
For more information on digital filter design, see,Į.g. Tools for FIR filter design inīoth Octave and the Matlab Signal Processing Toolbox are listed whereĪpplicable. Filter Designer enables you to quickly design digital FIR or IIR filters by setting filter performance specifications, by importing filters from your MATLAB ® workspace or by adding, moving, or deleting poles and zeros. Other methods, such as least-squares, are discussedīriefly to provide further perspective. Filter Designer is a powerful user interface for designing and analyzing filters.

The so-called `` window method'' for FIR filter design,Īlso based on the convolution theorem for Fourier transforms, isĭiscussed in some detail, and compared with an optimalĬhebyshev method. Filter Designer is a powerful graphical user interface (GUI) in Signal Processing Toolbox for designing and analyzing filters. This chapter provides a starting point in the area of FIR digitalįilter design. ASN Filter Designer provides engineers with everything they need to design, experiment and deploy complex IIR and FIR digital filters for a variety of sensor measurement applications. Designers can create an antisymmetric FIR filter that implements an odd function by. To make the most of FFT processorsįor FIR filter implementation, we will need flexible ways to design Symmetrical FIR filters implement even functions with symmetric tap adders. , replacing the DTFT with a (zero-padded) FFT, as In practice, the DTFT is used in sampled form, We give examples that illustrate how the proposed and the usual approaches differ, and how the new approach can be used to design filters with flat passbands, filters which meet point constraints, minimum-phase filters, and bandpass filters with controlled transition band behavior.As usual with the DTFT, the sampling rate is assumed to be
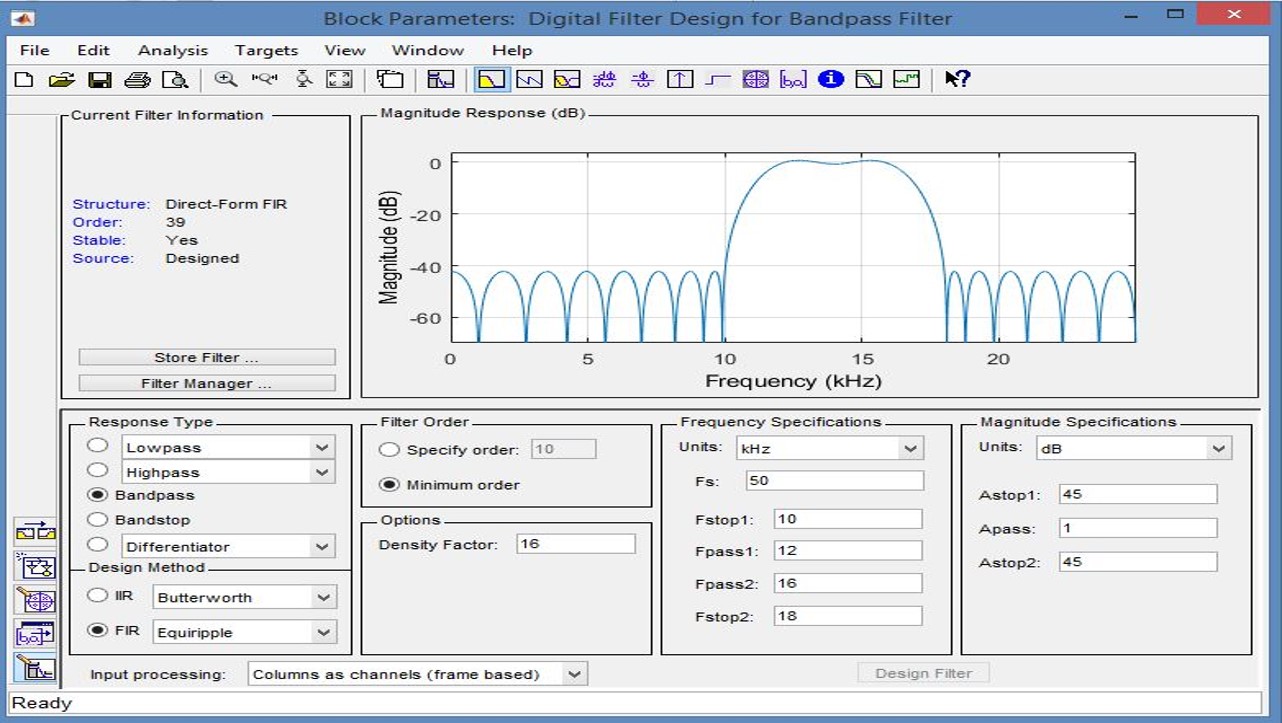
VeryĪt passband magnitude characteristics can be obtained by constraining the passband to be a concave-downward function. The simplex algorithm, while much slower than exchange algorithms, also allows us to incorporate more general kinds of constraints, such as constraints which force the magnitude response to be a concave function in a particular band. We use the simplex algorithmįor linear programming to find the best linear-phase FIR filter of minimum length, as well as to find the minimum feasible length itself. The resulting filter responses touch the constraint boundaries at many points, however, and are not good final designs because they do not make the best use of the degrees of freedom in the coefficients. Previous papers have described methods for using an exchange algorithm for finding a feasible linear-phase FIR filter of a given length if one exists, given upper and lower bounds on its magnitude response. In this paper we propose a different approach: specify the filter only in terms of upper and lower limits on the response, find the shortest filter length which allows these constraints to be met, and then find a filter of that length which is farthest from the upper and lower constraint boundaries in a mini-max sense. The FIR Filter Designer app designs minimal-order finite impulse response (FIR) digital filters based on performance specifications you provide.

The usual way of designing a filter is to specify a filter length and a nominal response, and then to find a filter of that length which best approximates that response.


 0 kommentar(er)
0 kommentar(er)
